Descripcion de un Dron
Un dron entra dentro de la categoría de los helicópteros debido a que se trata de una aeronave que es propulsada y sustentada a traves de uno o mas rotores los cuales se encuentran conformados por dos o mas palas
Mas específicamente un dron posee cuatro rotores capaces de producir una fuerza de empuje a una distancia determinada con relación al centro de gravedad del dron, donde a partir de la variación de la velocidad de los rotores es posible cambiar la magnitud de dichas fuerzas de sustentación, lo que le da a este la oportunidad de mantener un estado estacionario como si flotase en el aire o de mantener una determinada dirección de vuelo
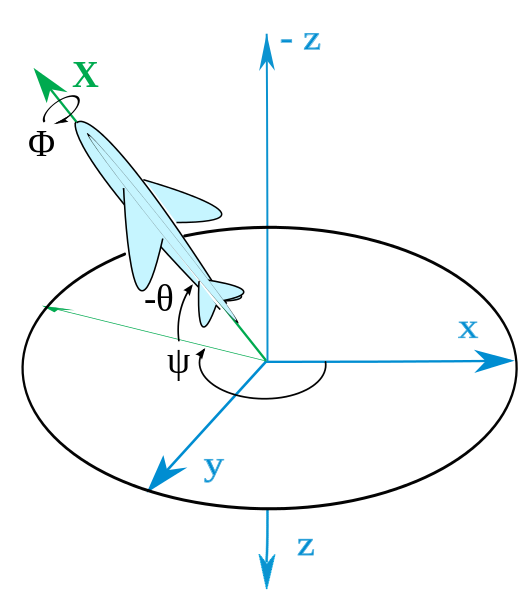
Dinamica del cuadrimotor
Matrices de conversion
Si se considera a los vectores \(\vec{x_b}\) como el marco de referencia o marco del dron y al vector \(\vec{x}\) como el marco inercial o terrestre, se puede emplear una matriz de rotación \(R\) que me permita realizar la conversión entre los distintos marcos [1].
\begin{equation}\nonumber \vec{x}= \begin{bmatrix} C\psi S\theta & C\psi S\theta S\phi - S\psi C\phi & C\psi S\theta C\phi + S\psi S\phi \\ S\psi C\theta & S\psi S\theta S\phi + C\psi C\phi & S\psi S\theta C\phi - C\psi S\phi \\ -S\theta & C\theta S\phi & C\theta C\phi \\ \end{bmatrix} *\vec{x_b} \end{equation} \begin{equation}\nonumber \vec{x}=R*\vec{x_b} \end{equation}La anterior matriz permite encontrar cual es la coordenada de un punto fijo en el marco rotado con referencia al marco inercial terrestre [1].
Debido a que R es una matriz ortogonal su inversa es igual a su transpuesta y por ende la matriz que permite encontrar la coordenada de un punto en el marco inercial con referencia a un punto en el marco del cuerpo queda expresada de la siguiente manera [1]:
\begin{equation}\nonumber \vec{x_b}= \begin{bmatrix} C\psi S\theta & S\psi C\theta & -S\theta \\ C\psi S\theta S\phi - S\psi C\phi & S\psi S\theta S\phi + C\psi C\phi & C\theta S\phi \\ C\psi S\theta C\phi + S\psi S\phi & S\psi S\theta C\phi - C\psi S\phi & C\theta C\phi \\ \end{bmatrix} *\vec{x} \end{equation} \begin{equation}\nonumber \vec{x_b}=R^T*\vec{x} \end{equation}
Fuerza de empuje
La fuerza de empuje \(T\) producto de las fuerzas combinadas de los motores y las hélices siempre están ubicados en el eje z del aeromodelo [2].
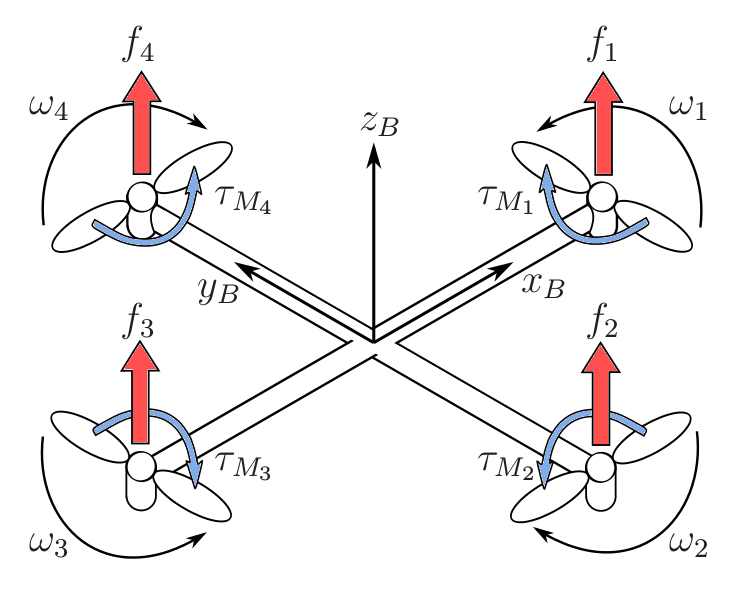[2]
\begin{equation}
T = \sum_{i=1}^{4}fi=b\sum_{i=1}^{4}(\Omega_i)^2 \quad , \quad
T_B= \begin{bmatrix} 0 \\ 0 \\ T \end{bmatrix}
\end{equation}
Torque
El torque \(\tau_B\) producto de la fuerza de empuje se encuentra compuesto por los torques \(\tau_\phi \ \tau_\theta \ \tau_\psi\) en la dirección de sus respectivos ángulos con relación al cuerpo del cuadrimotor [2].
\begin{equation}\nonumber \tau_B = \begin{bmatrix} lb[-(\Omega_2)^2+(\Omega_4)^2] \\ lb[-(\Omega_1)^2+(\Omega_3)^2] \\ d[-(\Omega_1)^2+(\Omega_2)^2-(\Omega_3)^2+(\Omega_4)^2] \\ \end{bmatrix} = \begin{bmatrix} \tau_\phi \\ \tau_\theta \\ \tau_\psi \end{bmatrix} \end{equation}El efecto de estos torques se vera manifestado en los movimientos de alabeo cabeceo (pitch \(\theta\)), alabeo (roll \(\phi\)) y guiñada (yaw \(\psi\)) [2].
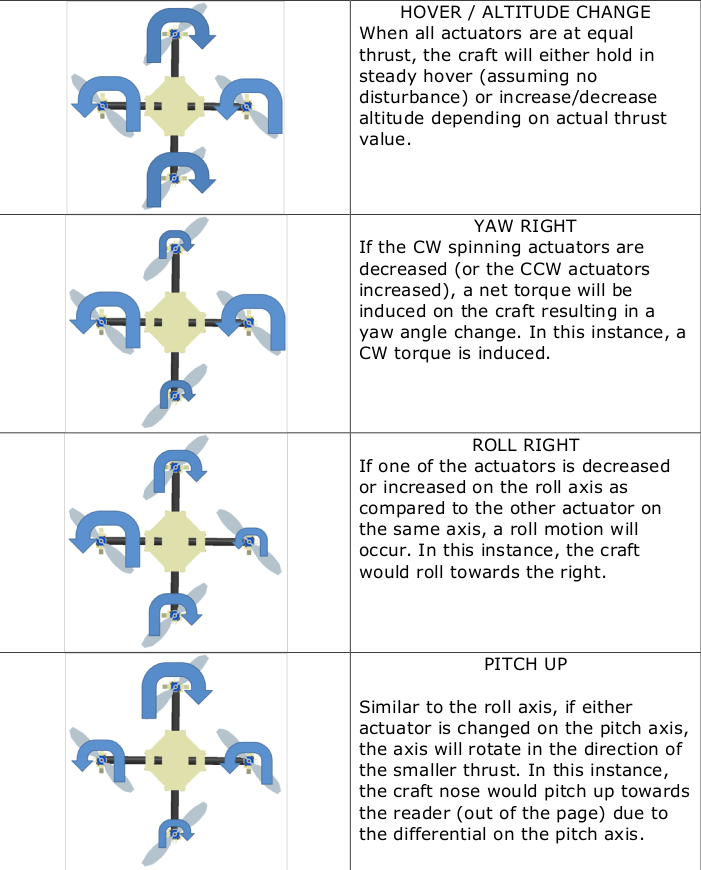[3]
Ecuaciones del sistema
La fuerza requerida para acelerar la masa mas la fuerza centrifuga es igual a la fuerza de gravedad mas la fuerza de empuje producto de los motores [2].
\begin{equation}\label{movimiento-dron} m\dot{V_B}+\nu\times(mV_B)=R^TG+T_B \end{equation}La gran mayoria de las fuerzas se encuentran dentro de los ejes del aeromodelo, sin embargo el vector de gravedad siempre se encuentra fijo con respecto al eje terrestre por ende es necesaria la matriz de rotación [3]
Por otra parte en el marco inercial la fuerza centrifuga es nula y por ende puede obtenerse [2]:
\begin{equation} \begin{aligned}\label{prueba} mR\dot{V_B}=RR^TG+RT_B \\ m\dot{V}+=G+RT_B \end{aligned} \end{equation}Controlador
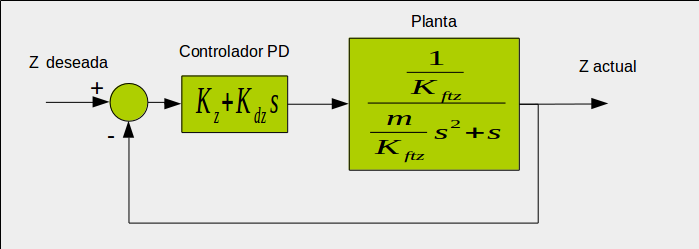
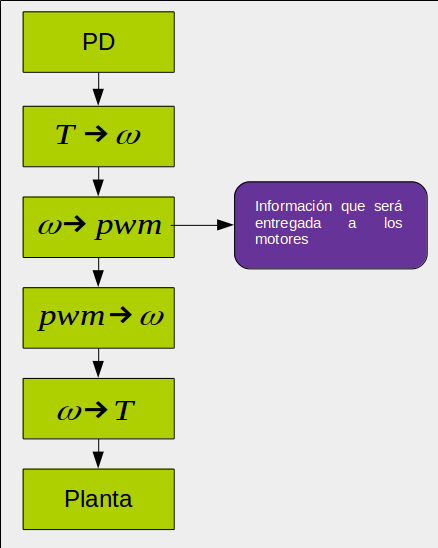
Descripcion de los elementos a utilizar
nrf24l01
motor
control
everloop
PWM
iNEMO
I2C
matrix creator
Diagrama general del sistema
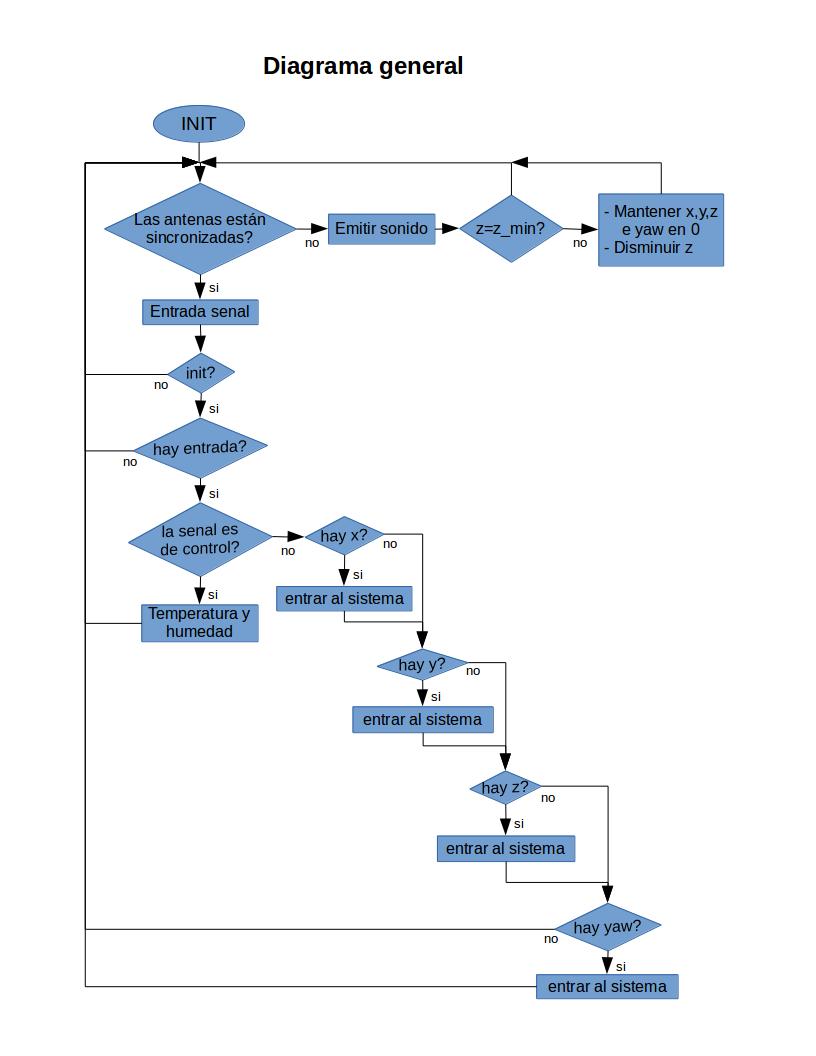
Bibliografía
- MIT Kinematics of moving frames () recuperado de link
- Luukkonen. T, (2011). Modelling and control of quadcopter (1ra Ed.). recuperado de link recuperado el 5 de Noviembre de 2016.
- Schmidt. M., (2011).Simulation and control of a quadrotor unmanned aerial vehicle. Disponible en link recuperado el 6 de Noviembre de 2016.
- Horace, Ode; quoted from Horace: The Complete Odes and Epodes, (trans.) () West D.; reprinted in Fear, T (ed.) Reputations (AA100 Book 1), Milton Keynes, The Open University, p. 28. Fear, T. (ed) Reputations (AA100 Book 1), Milton Keynes, The Open University, p.13.